Difference between revisions of "Component: Fast Fourier Transform (FFT) (DSP)"
| (2 intermediate revisions by the same user not shown) | |||
| Line 14: | Line 14: | ||
==Fast Fourier Transform (FFT) component== | ==Fast Fourier Transform (FFT) component== | ||
Provides a way of converting a buffer full of time domain data into frequency domain data. The output of the FFT is a set of frequency bins which correspond to the frequencies present in the signal. The number of frequency bins is equal to half the input buffer size with each bin being responsible for a portion of the frequency up to 1/2 the nyquist. | Provides a way of converting a buffer full of time domain data into frequency domain data. The output of the FFT is a set of frequency bins which correspond to the frequencies present in the signal. The number of frequency bins is equal to half the input buffer size with each bin being responsible for a portion of the frequency up to 1/2 the nyquist. | ||
| + | |||
| + | ==Component Pack== | ||
| + | |||
| + | DSP | ||
==Detailed description== | ==Detailed description== | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| Line 24: | Line 34: | ||
==Examples== | ==Examples== | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| Line 102: | Line 118: | ||
|- | |- | ||
|- | |- | ||
| − | | width="10%" align="center" | [[File:]] - | + | | width="10%" align="center" | [[File:Fc9-bool-icon.png]] - BOOL |
| width="90%" | ProcessWhenFull | | width="90%" | ProcessWhenFull | ||
|- | |- | ||
| colspan="2" | 0 = Do Nothing when Buffer is full, 1 = Auto call FFT macro when Buffer is full | | colspan="2" | 0 = Do Nothing when Buffer is full, 1 = Auto call FFT macro when Buffer is full | ||
|- | |- | ||
| − | | width="10%" align="center" style="border-top: 2px solid #000;" | [[File:]] - | + | | width="10%" align="center" style="border-top: 2px solid #000;" | [[File:Fc9-bool-icon.png]] - BOOL |
| width="90%" style="border-top: 2px solid #000;" | ''Return'' | | width="90%" style="border-top: 2px solid #000;" | ''Return'' | ||
|} | |} | ||
| Line 122: | Line 138: | ||
|- | |- | ||
|- | |- | ||
| − | | width="10%" align="center" | [[File:Fc9-type- | + | | width="10%" align="center" | [[File:Fc9-type-16-icon.png]] |
| width="90%" | Connect To | | width="90%" | Connect To | ||
|- | |- | ||
| − | | colspan="2" | | + | | colspan="2" | DSP component with output buffer to collect our data from. |
|- | |- | ||
| width="10%" align="center" | [[File:Fc9-type-21-icon.png]] | | width="10%" align="center" | [[File:Fc9-type-21-icon.png]] | ||
| Line 141: | Line 157: | ||
|- | |- | ||
| colspan="2" | Applies a hamming window filter to the time domain sample data to provide better frequency detection. | | colspan="2" | Applies a hamming window filter to the time domain sample data to provide better frequency detection. | ||
| + | |- | ||
| + | | width="10%" align="center" style="background-color:#EAE1EA;" | [[File:Fc9-conn-icon.png]] | ||
| + | | width="90%" style="background-color:#EAE1EA; color:#4B008D;" | Calculations | ||
| + | |- | ||
|- | |- | ||
| width="10%" align="center" | [[File:Fc9-type-15-icon.png]] | | width="10%" align="center" | [[File:Fc9-type-15-icon.png]] | ||
| Line 161: | Line 181: | ||
|- | |- | ||
| colspan="2" | The frequency range covered by each frequency bin. | | colspan="2" | The frequency range covered by each frequency bin. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|} | |} | ||
Latest revision as of 17:19, 9 November 2022
| Author | Matrix Ltd |
| Version | 1.2 |
| Category | DSP |
Contents
Fast Fourier Transform (FFT) component
Provides a way of converting a buffer full of time domain data into frequency domain data. The output of the FFT is a set of frequency bins which correspond to the frequencies present in the signal. The number of frequency bins is equal to half the input buffer size with each bin being responsible for a portion of the frequency up to 1/2 the nyquist.
Component Pack
DSP
Detailed description
No detailed description exists yet for this component
Examples
Example takes two adjustable frequency sine wave inputs and combines them and then passes the collection of 256 samples to the FFT function which produces 128 individual frequency banks which are then plotted from left (lowest frequency) to right (highest frequency) using an XY chart component.
Frequency output for a set of data
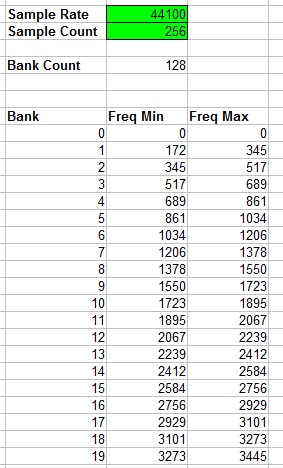
Frequency banks can be worked out by using the sample frequency and buffer size. The number of frequency banks is equal to the number of samples divided by 2 minus 1. We subtract the one because bank 0 is always empty and so can be discounted.
FrequencyBanks = (SampleCount / 2) - 1
The frequency ranges present inside a bank can be worked out as follows.
FreqMin = ((SampleRate / 2) / (SampleCount / 2)) * Bank
FreqMax = ((SampleRate / 2) / (SampleCount / 2)) * (Bank + 1)
For example if we sample at 10KHz and collect 256 samples then frequency bank 10 would represent any frequencies in the range of 390.6Hz to 429.7Hz.
Here is a spreadsheet document that will calculate the frequencies present in each bank. The highlighted green fields are editable and will update the rest of the values.
File:FFT Frequency Bank Calculator.xls
Downloadable macro reference